Algebra relazionale

1. Introduzione

Alcuni link Importanti:

• La teoria degli insiemi: La teoria degli insiemi
• Le basi di dati: Database
• Wikipedia: Algebra relazionale

Definizione (di Wikipedia):

In informatica l’algebra relazionale e il collegato calcolo relazionale fanno parte dell’insieme di linguaggi che permettono di esaminare le query (interrogazioni) da effettuare nell’ambito della gestione/utilizzo di un database. (da Wikipedia).

2. Tabelle Esempi

Per gli esempi successivi prendiamo in considerazione queste tabelle:

• Tabella PERSONE:

  Nome	Cognome	Sesso	Matricola
  Adrian	Neri	M	9297
  Mirco	Neri	M	7432
  Giada	Verdi	F	9824
  Marta	Bianchi	F	9858

• Tabella PROGETTI:

  Nome_P	Numero_P	Sede_P	Numero_D
  ProgettoX	1	Bellaire	5
  ProgettoY	2	Sugarland	5
  ProgettoZ	3	Houston	5
  Informatizzazione	10	Salford	4
  Riorganizzazione	20	Houston	1
  nuove opportunità	30	Salford	4

• Tabella SEDI_DIPARTIMENTO:

  Numero_D	Sede_D
  1	Houston
  4	Salford
  5	Bellaire
  5	Sugarland
  5	Houston

• Tabella LAURETATI:

  Matricola	Nome	Età
  7274	Rossi	42
  7432	Neri	54
  9824	Verdi	45

• Tabella SPECIALISTI:

  Matricola	Nome	Età
  9297	Neri	33
  7432	Neri	54
  9824	Verdi	45

3. Operatori

Gli operatori si suddividono in 2 categorie principali:

Nota: gli operatori di: Selezione, Proiezione, Ridenominazione, Unione, Differenza, Prodotto Cartesiano sono operatori di base (primitivi). Mentre i restanti 3 (intersezione, join, divisione) sono derivati dai primi 6.

• Operatori Unari:
  • Selezione;
  • Proiezione;
  • Ridenominazione.
• Operatori Binari:
  • Unione;
  • Differenza;
  • Prodotto Cartesiano;
  • Intersezione;
  • Join;
  • Divisione.

3.1 Selezione

La selezione è un operatore unario ortogonale dell’algebra relazionale che seleziona le tuple di una relazione (tabella) che soddisfano una particolare condizione. Il simbolo della selezione è sigma $σ$ o SEL.

$$σ_{condizione}(relazione)$$

oppure:

$$SEL_{condizione}(relazione)$$

Il risultato della selezione è una tabella con lo stesso schema della relazione r(X) in ingresso. Dove X è l’insieme degli attributi.

Nota: La selezione si dice operatore “ortogonale” perché seleziona le righe della tabella che soddisfano la condizione specificata, senza duplicazioni, mantenendo gli stessi attributi (X).

• esempio 1: Trovare i progetti sviluppati nella sede di Huston:

  Soluzione: $SEL_{SEDE\_P=HUSTON}(PROGETTO)$

  il risultato di questa query sarà:

  Sede_P
  Houston
  Houston

• esempio 2: Trovare il nome dei progetti e il numero di dipartimenti dei progetti sviluppati nella sede di Huston:

  Soluzione: $PROJ_{NOME\_P,\ NUM\_D}(SEL_{SEDE\_P=HUSTON}(PROGETTO))$

  il risultato di questa query sarà:

  Nome_P	Numero_D
  ProgettoZ	5
  Riorganizzazione	1

3.2 Proiezione

La proiezione è un operatore unario ortogonale dell’algebra relazionale che seleziona alcuni attributi (colonne) di una relazione (tabella). Il simbolo della proiezione è la pi greco $\pi$ con in pedice la lista degli attributi e tra parentesi il nome della relazione:

$$\pi_{attrributi}(relazione)$$

oppure:

$$PROJ_{attrributi}(relazione)$$

Il risultato della proiezione è una tabella contenente al più tutte le ennuple della relazione in ingresso senza duplicazioni ma soltanto alcune colonne.

• esempio: Trovare il nome e il cognome delle persone:

  Soluzione: $PROJ_{NOME,\ COGNOME}(PERSONE)$

  il risultato di questa query sarà:

  Nome	Cognome
  Adrian	Neri
  Mirco	Neri
  Giada	Verdi
  Marta	Bianchi

---

3.3 Ridenominazione

La ridenominazione è un operatore unario dell’algebra relazionale che permette di cambiare i nomi degli attributi di una relazione R. Il simbolo è $\rho$:

$$\rho_{nuovonome \leftarrow nomeattributo}(relazione)$$

oppure:

$$REN_{nuovonome \leftarrow nomeattributo}(relazione)$$

L’operazione di ridenominazione cambia soltanto i nomi degli attributi nello schema della relazione e non i dati nelle tuple.

Il contenuto della tabella resta tale e quale.

• esempio 1: Rinominare l’attributo “Nome” della tablella SPECIALISTI in “Cognome”:

  Soluzione: $REN_{Cognome \leftarrow Nome}(SPECIALISTI)$

  il risultato di questa query sarà:

  Matricola	Cognome	Età
  9297	Neri	33
  7432	Neri	54
  9824	Verdi	45

• esempio 2: Rinominare l’attributo “Nome” della tablella SPECIALISTI in “Cognome” e l’attributo “Età” in Anni:

  Soluzione: $REN_{Cognome,Anni \leftarrow Nome, Età}(SPECIALISTI)$

  il risultato di questa query sarà:

  Matricola	Cognome	Anni
  9297	Neri	33
  7432	Neri	54
  9824	Verdi	45

  ---

3.4 Unione

• In matematica: In termini rigorosi l’unione di due insiemi $A, \ B \subseteq \ E$ contenuti in un insieme universo $E$ é l’insieme contenente tutti gli elementi dell’insieme $A$ e tutti gli elementi dell’insieme $B$. II simbolo di unione $\cup$, dunque indichiamo runione tra gli insiemi $A,\ B$ con la notazione:

  $$A \cup B$$

  La definizione di unione insiemistica in simboli é data dalla seguente rappresentazione per caratteristica:

  $$A \cup B := \{ x \in E \ | \ x \in A \ \vee x \in B \}$$

  • esempio: Consideriamo come insieme universo $E = \{1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8, \ 9, \ 10\}$:

    e i seguenti suoi sottoinsiemi:

    $B = \{3, \ 4, \ 5\}$

    $D = \{8, \ 10\}$

    Quanto fa $B \cup D$?

    RISPOSTA:

    $B \cup D = \{3, \ 4, \ 5\} \cup \{8, \ 10\} = \{ 3, \ 4, \ 5, \ 8, \ 10\}$

• In Algebra Relazionale: L’unione è un operatore insiemistico binario dell’algebra relazionale che unisce due relazioni r1 e r2 (tabelle) in un’unica relazione r3. Il simbolo dell’unione è $\cup$.

  $$r_3 = r_1 \ \cup \ r_2$$

  Le due relazioni operandi r1 e r2 devono avere lo stesso numero e tipo (dominio) di attributi da sinistra verso destra, ossia tuple omogenee.

  Il risultato è una relazione unione r3 composta da tutte le tuple delle due relazioni, senza duplicazioni.

  • esempio 1: Eseguire l’unione tra Laureati e Specialisti:

    Soluzione: $Laureati \cup Specialisti$

    il risultato di questa query sarà:

    Matricola	Nome	Età
    7274	Rossi	42
    7432	Neri	54
    9824	Verdi	45
    9297	Neri	33

  • esempio 2: Eseguire l’unione tra Laureati e Specialisti proiettando solo la matricola:

    Soluzione: $PROJ_{Matricola}(Laureati \cup Specialisti)$

    il risultato di questa query sarà:

    Matricola
    7274
    7432
    9824
    9297

    Nota: Naturalmente l’unione viene eseguita anche sugli altri attributi, ma stiamo proiettando solo la matricola.

---

3.5 Differenza

• In matematica: La differenza tra due insiemi $A,\ B \subseteq E$ contenuti in un insieme universo $E$ é per definizione l’operazione che sottrae agli elementi del primo insieme $A$ gli elementi del secondo insieme $B$. II simbolo della differenza insiemistica é il meno -, o in alternativa la barra discendente \ così che l’insieme differenza tra $A$ e $B$ si indica in modo equivalente come:

  $$A - B \ \ \ ; \ \ \ A\setminus B$$

  Se volessimo descrivere la differenza insiemistica mediante simboli, potremmo scrivere:

  $$A - B := \{ x \in E \ | \ x \in A \ \wedge x \notin B \}$$

  • esempio: Consideriamo come insieme universo $E = \{1, \ 2, \ 3, \ 4, \ 5, \ 6, 7, \ 8, \ 9, \ 10\}$:

    e i seguenti suoi sottoinsiemi:

    $A = \{1, \ 3, \ 5, \ 7\}$

    $B = \{1, \ 3, \ 8, \ 9\}$

    Quanto fa $A - B$?

    RISPOSTA:

    $A - B = \{1, \ 3, \ 5, \ 7\} - \{1, \ 3, \ 8, \ 9\} = \{ 5, \ 7\}$

• In Algebra Relazionale: La differenza è un operatore insiemistico binario dell’algebra relazionale che contiene le tuple presenti nella relazione r1, ma non nella relazione r2:

  $$r_3 = r_1 - r_2$$

  Le due relazioni operandi r1 e r2 hanno tuple omogenee. In pratica, le due tabelle hanno lo stesso numero di attributo e lo stesso dominio degli attributi visti da sinistra verso destra.

  Il risultato della differenza è una relazione composta dalle tuple presenti nella prima relazione ma non nella seconda.

  Nota Bene: è possibile eseguire l’operazione di differenza tra 2 tabelle se e solo se hanno lo stesso schema

  • esempio: Eseguire la differenza tra Laureati e Specialisti:

    Soluzione: $Laureati - Specialisti$

    il risultato di questa query sarà:

    Matricola	Nome	Età
    7274	Rossi	42

---

3.6 Prodotto Cartesiano

• In matematica: Il prodotto cartesiano è un’operazione tra due insiemi. Dati due insiemi $A$ e $B$, il prodotto cartesiano $AxB$ è l’insieme di tutte le coppie ordinate $(a, b)$ dove il primo elemento $"a"$ appartiene all’insieme $A$ e il secondo elemento $"b"$ appartiene all’insieme $B$.

  

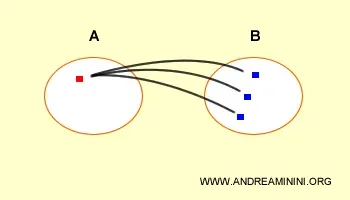
  il prodotto cartesiano è definito in questo modo:

  $$AxB := \{(a,b)\ |\ a\in A,\ b\in B\}$$

  Si legge “A per B” oppure “A cartesiano B”.

  • esempio: Prendo in considerazione due insiemi A e B composti da due e tre elementi.

    $A = \{1, \ 3\}$

    $B = \{2, \ 4, \ 6\}$ Il prodotto cartesiano AxB risulterà:

    $AxB = \{ (1, \ 2), \ (1, \ 4), \ (1, \ 6), \ (3, \ 2), \ (3, \ 4), \ (3, \ 6) \}$

• In Algebra Relazionale: Il prodotto cartesiano è un operatore binario insiemistico dell’algebra relazionale che, date due relazioni r1 e r2, crea una relazione composta da tutte le combinazioni possibili delle tuple della prima con le tuple della seconda. Il simbolo del prodotto cartesiano è $X$:

  $$r_3 = r_1 \ X \ r_2$$

  Nel prodotto cartesiano ogni tupla della prima relazione è seguita da tutte le tuple della seconda relazione.

  E’ un operatore insiemistico perché ha lo stesso significato matematico del prodotto cartesiano nella teoria degli insiemi.

  • esempio: Trova il prodotto cartesiano fra PERSONE e LAUREATI:

    Soluzione: $PERSONE \ X \ LAUREATI$

    il risultato di questa query sarà:

    Nome	Cognome	Sesso	Matricola	Matricola_L	Nome_L	Età_L
    Adrian	Neri	M	9297	7274	Rossi	42
    Adrian	Neri	M	9297	7432	Neri	54
    Adrian	Neri	M	9297	9824	Verdi	45
    Mirco	Neri	M	7432	7274	Rossi	42
    Mirco	Neri	M	7432	7432	Neri	54
    Mirco	Neri	M	7432	9824	Verdi	45
    Giada	…	…	…	…	…	…
    …	…	…	…	…	…	…

  • esempio: Trova il prodotto cartesiano fra PERSONE e LAUREATI, questa volta estraendo solo le tuple significative:

    Soluzione: $SEL_{Matricola\_P = Matricola\_L} (PERSONE \ X \ LAUREATI)$

    il risultato di questa query sarà:

    Nome	Cognome	Sesso	Matricola	Matricola_L	Nome_L	Età_L
    Mirco	Neri	M	7432	7432	Neri	54
    Giada	Verdi	F	9824	9824	Verdi	45

---

3.7 Intersezione

• In matematica: Consideriamo due insiemi $A, \ B \subseteq E$ contenuti in un insieme universo $E$. Definiamo l’intersezione tra gli insiemi $A, \ B$ come l’insieme degli elementi appartenenti a entrambi gli insiemi, ossia degli elementi in comune tra di essi. II simbolo di intersezione é $\bigcap$ , quindi per indicare I’intersezione tra $A$ e $B$ scriviamo:

  $$A \ \bigcap \ B$$

  Possiamo tradurre la definizione di intersezione insiemistica in simboli nel seguente modo:

  $$A \ \bigcap \ B := \{ x \in E \ | \ x \in A \ \wedge \ x \in B \}$$

  • esempio: Consideriamo come insieme universo $E = \{1, \ 2, \ 3, \ 4, \ 5, \ 6, 7, \ 8, \ 9, \ 10\}$:

    e i seguenti suoi sottoinsiemi:

    $A = \{1, \ 2, \ 3 \}$

    $B = \{3, \ 4, \ 5\}$

    Quanto fa $A \ \bigcap \ B$?

    RISPOSTA:

    $A \ \bigcap \ B = \{1, \ 2, \ 3 \} \ \bigcap \ \{3, \ 4, \ 5\} = \{3\}$

• In Algebra Relazionale: L’intersezione è un operatore insiemistico binario dell’algebra relazionale che seleziona le tuple in comune in due relazioni r1 e r2 (tabelle). Il simbolo dell’intersezione è $⋂$.

  $$r_3 = r_1 ⋂ r_2$$

  Le due relazioni operandi r1 e r2 hanno tuple omogenee, ossia lo stesso numero e tipo (dominio) di attributi visti da sinistra verso destra.

  Il risultato dell’intersezione è una relazione composta dalle tuple presenti in entrambe le relazioni, senza duplicazioni.

  • esempio: Eseguire l’intersezione tra LAUREATI e SPECIALISTI:

    Soluzione: $LAUREATI ⋂ SPECIALISTI$

    il risultato di questa query sarà:

    Matricola	Nome	Età
    7432	Neri	54
    9824	Verdi	45

---

3.8 Join

L’operatore join in algebra relazionale correla i dati contenuti in relazioni diverse confrontando i valori. Esistono due tipi di join: il join naturale e il join condizionale (theta join).

Si tratta di un operatore che ha per operandi una o due relazioni (tabelle) in ingresso e fornisce in uscita un’altra relazione (tabella).

3.8.1 Join Naturale

Il join naturale correla i dati in due relazioni diverse sulla base dei valori uguali negli attributi con lo stesso nome. Il simbolo del join naturale è una “farfalla” $⋈$.

$$r1⋈r2 = {t \in X_1 \ \cup \ X_2 \ | \ t[X_1] \in r_1 \wedge t[X_2] \in r_2}$$

Il presupposto è che ci siano due relazioni contenenti alcuni attributi con lo stesso nome.

3 casi:

• Join completo: Il join si dice completo se ogni tupla di ciascuna relazione degli operandi contribuisce almeno a una tupla del risultato.
• Join incompleto: Il join si dice incompleto se almeno una tupla delle relazioni degli operandi non contribuisce al risultato.
• Join vuoto: Il join si dice vuoto se nessuna tupla delle relazioni degli operandi contribuisce al risultato finale.

Nota: Se nel join naturale non ci sono attributi in comune, il risultato è il prodotto cartesiano delle relazioni r1 x r2.

Nota: Se nel join naturale tutti gli attributi in comune, il risultato è l’intersezione delle relazioni r1 x r2.

3.8.2 Theta Join

Il join condizionale (theta join) correla i dati in due relazioni diverse sulla base di una condizione booleana. E’ anche detto theta join. Il simbolo del join condizionale è una farfalla seguita da una C:

$$r1⋈_Cr2$$

L’operatore theta join legge le tuple della prima relazione e verifica quali tuple della seconda relazione soddisfano la condizione di join.

Se la condizione è soddisfatta le tuple sono combinate e aggiunte nella tabella di join.

Viceversa, le tuple che non la soddisfano sono escluse.

Nota: Il join condizionale tra due relazioni r1 e r2 equivale a una selezione sul prodotto cartesiano delle relazioni r1 X r2.

• esempio: Eseguire la Join tra PERSONE e SPECIALISTI:

  Soluzione: $PERSONE ⋈_{Matricola\_P=Matricola\_S} (SPECIALISTI)$

  il risultato di questa query sarà:

  Nome	Cognome	Sesso	Matricola	Matricola_S	Nome_S	Età_S
  Adrian	Neri	M	9297	9297	Neri	33
  Mirco	Neri	M	7432	7432	Neri	54
  Giada	Verdi	F	9824	9824	Verdi	45

  Nota: colorati in blu gli attributi e le tuple appartenenti alla tebella SPECILISTI.

---

3.9 Divisione

La divisione è un operatore binario dell’algebra relazionale che contiene le tuple <x> della prima relazione A tali che per ogni tupla <y> della seconda relazione B ci sia una tupla <x,y> nella prima relazione:

$$A \ / \ B= \{ <x> \ | \ \ ∀<y> \ ∈B,<x,y> \ ∈A \}$$

Si tratta di un operatore derivato perché si ottiene combinando altri operatori primitivi dell’algebra relazionale.

$$A \ / \ B = ∏_x(A) - N$$

Dove N sono i valori interdetti di A ossia quei valori <x> di A che associati a <y> di B formano una tupla <x,y> non presente in A.

$$N = ∏_x((∏_x(A) * B)-A)$$